Анализ влияния ошибок установки колёсных пар на точность обработки при точении

03.03.2020
в Наука, Статьи

Анализ влияния ошибок установки колёсных пар на точность обработки при точении https://volopro.ru/wp-content/uploads/2019/07/feature-69-1920x12821.jpg 1920 1282 Volo Volo //volopro.ru/wp-content/uploads/2022/10/VOLOpro_logo-2.png 03.03.2020 12.09.2022

Обработка колёсных пар вращения на токарных станках может быть затруднена вследствие массогабаритных параметров самих деталей. Их сложно разместить на токарном станке обычной конструкции и закрепить в шпинделе. Существуют станки, которые выполняют токарные операции без жесткой фиксации детали в шпинделе. Деталь приводится во вращение внешним приводом посредством фрикционной передачи (один из возможных способов) [1].

Вследствие отсутствия жесткой привязки базовых поверхностей детали к базовым поверхностям и осям станка могут возникнуть установочные или монтажные перекосы, рисунок 1.

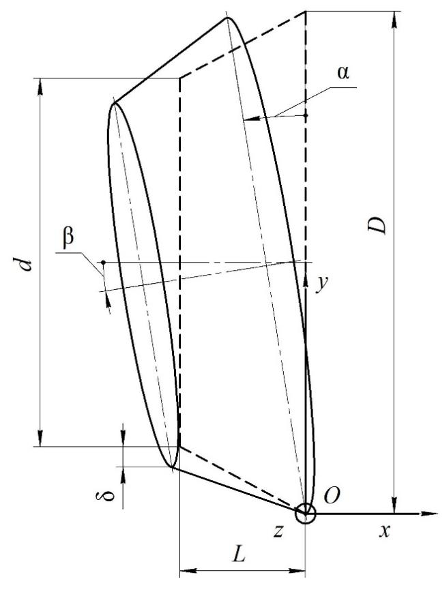
Рисунок 1 – Ошибки расположения детали

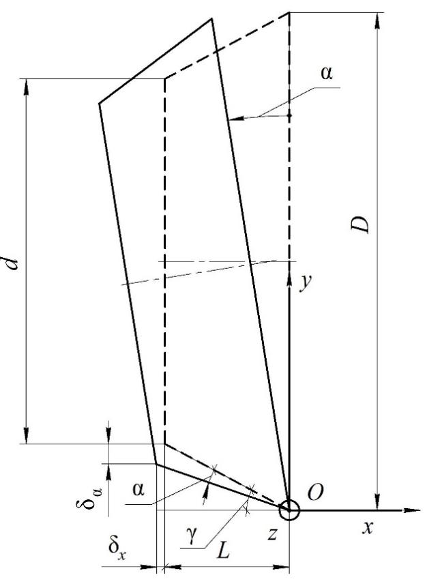
Рисунок 2 – Влияние угла поворота α на ошибку при точении

На рисунке штриховыми линиями показано идеальное положение детали по отношению к базовым поверхностям и осям станка. Для общего случая определения ошибок выбрана коническая поверхность вращения. С ней связана декартовая система координат Oxyz. Считаем, что начало отчета O является базовой точкой для начального положения резца. В этом случае, возможно отклонение детали в виде перекосов: поворот вокруг оси Oz на угол α, поворот вокруг оси Oy на угол β [2-4].

Если резец при обработке будет двигаться вдоль идеальной поверхности детали, строго заданной уравнениями в системе отчета станка, то реальная деталь будет обтачиваться с ошибкой, которая будет увеличиваться в направлении вдоль оси Ox (в области отрицательных координат оси Ox). Суммарная ошибка на рисунке 1 обозначена δ. Как видно, эта ошибка обеспечивает уменьшение радиуса обточки детали при выбранных направлениях погрешностей установки [5-10].

Определим ошибку радиуса и диаметра обточки в зависимости от погрешностей установки. Если имеется только поворот вокруг оси Oz на угол α, рисунок 2, то имеем только одну ошибку δ_α

Если деталь имеет толщину L, диаметры большего и меньшего оснований усеченного конуса соответственно D и d, тогда угол наклона образующей равен

$\gamma=arctg\left(\frac{D-d}{2L}\right)$

(1)

Максимальная погрешность радиуса будет находится на меньшем основании усеченного конуса и определяться

$\delta_a=L\big(tan\gamma-tan(\gamma-\alpha)\big)$

(2)

Однако, мы видим, что имеется еще и смещение δ_x вдоль оси Ox:

$\delta_x=L\big(cos\gamma-cos(\gamma-\alpha)\big)$

(3)

Тогда подставляем (3) в выражение (2) и фактическая ошибка радиуса сечения кругового конуса составляет:

$\delta_\alpha^\phi=L\big(tan\gamma-\big(1-(cos\gamma-cos(\gamma-\alpha))\big)tan(\gamma-\alpha)\big)$

(4)

Для произвольного сечения, определяемого координатой х (берем по модулю)

$\delta_{\alpha x}^\phi=x(tan\gamma-(1-(cos\gamma-cos(\gamma-\alpha))\big)tan(\gamma-\alpha)\big)$

(5)

Оценим погрешность δ^φ_αx при следующих параметрах: D = 600 мм, d = 500 мм, L = 150 мм, α = 2°. Получаем

$\gamma=arctg\left(\frac{600-500}{2•150}\right)=18,4°$

$\delta_\alpha^\phi=150(tan18,4°-(1-(cos18,4°-cos(18,4°-2°))\big)tan(18,4°-2°)\big)=5,29 мм$

Максимальная ошибка радиуса составляет – 5,29 мм, а ошибка диаметра – 10,58 мм.

Аналогично определяется ошибка при погрешности установки с поворотом вокруг оси Oz на угол β. Указанные ошибки могут складываться и вычитаться.

Таким образом, отмеченные погрешности установки крупногабаритных деталей по отношению к базовым поверхностям и осям станка имеют существенное значение на точность обработки. Если обработка производится на станках под управлением опытного станочника, то он может в процессе точения нивелировать эту погрешность. Для станков с ЧПУ необходимо устранять начальные погрешности или вносить поправки на эти погрешности в программу обработки.